Hello everyone
-
-
It has been a long time since my last journal but this is certainly a heartsome and fascinating one, over the last few weeks I have been working behind the blogger on the crane design that you ALL should now able to see. This jouinal is in celebration of a few things. Firstly, my dream crane "Super-Ken 2000" has been finished, and it will be coming into use at my home a while later. Secondly, I learnt a lot as designing a crane that brought real-world design problems into my life, each problem coming up in the working stages provided good opportunity with me to review and apply knowledge essential for a job in science and engineering. The third thing which is the last one and is worth celebrating one, I gained rich experience throught the hands-on activities.. including market research, cost management, work planing and whatnot here.
-(1) Introduction
Super-Ken 2000 is a family crane having a kind and sincere heart, its body is made of mild steel, and is composed of steel pipes, manual winch, steel wire and a custome-made trolley. In all honesty, Super-ken 2000 is designed mainly for helping my mother to pick up the giant tortoises (2 Sulcata tortoises), my mother who needs to take them back and forth twice per day from the living room to the bathroom. Speaking of the handling posture, I have ever suffered from severe backache several months ago. Indeed, pain in my back gave me a unhappy experience, not only backache was physical painful, it badly affected my daily life, mood, working capacity and efficiency. The people said: back is an essential and vital bone of the body also known as the life bone, I don't want my worst experience in back that will probably recur to my mother.-
-
-
(2) Super-Ken 2000 can become an expectant helper
My dream crane has enough capacity to lift a tortoise weighting 110 lbs (at approximately 50Kg), its completion will enable to prevent my mother from getting any possible damage in back, hand or any parts of body. Wishfully, I hope Super-Ken 2000 can become an expectant helper. -
Unbelievable but true, when I put my hand on the crane's body, I can feel the crane's heart beating. Shh.... Don't tell other people, Super-Ken 2000 is a humanoid crane, it has feeling, heartbeating and has a kind heart!..... I made it live!
-
-
Unbelievable but true, when I put my hand on the crane's body, I can feel the crane's heart beating. Shh.... Don't tell other people, Super-Ken 2000 is a humanoid crane, it has feeling, heartbeating and has a kind heart!..... I made it live!
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Photo Sharing:
To view the large picture, please click on the thumbnail.
- Hand winch equipped with spur gear and locking device for load control.
- - Super-Ken 2000 can be folded down for storage or transport
- - Super-Ken 2000 can rotate different degrees and its boom can extend 150mm more for special case.
- - Super-Ken 2000 is a family crane but only for tortoises.
- - Super-Ken 2000 is a kind crane, it likes working with elderly or housekeeper.
- - Super-Ken 2000 is made in Wong Tai Sin and designed by Ken Ngan.
-
(3) What I learnt most and challenges I faced
The most important challenge I faced was the intense workload accompanied with limited time. I frequently faced the timed works and felt truly that they were pretty heavy. The so-called "One-Man-Band Project" was nothing more than one person to do one thing until it to the end. Encouragingly, a man behind the "One-Man-Band Project" is called "Frank Lai", he is one great friend of mine, Lai gave me more productive ideas and led me on finding out the right or possible right things. Needless to say anything, all of his ideas of course were coming from his views and hands-on experience. He merely was a talker, not to take part in any work, but his advice did work very well to my thought and did help pushing forward to my works. I realized a lot by doing this so-called One-Man-Band Project, from a drafting to a working drawing, from ambiguity in the beginning to understanding in the end, and from a dream to realization as well. It was worthwhile to experience all these!
-
Apart from the above-mentioned, I learnt how to handle time on the manufacturing process to a lifting crane, yet I learnt most in the working stages should be sending understanding and accepatance to the manufactuer's works, not to discredit their workmanship, most of all did not follow my drawing to do... for example: (i) a 2" steel pipe, it was considered to be main mast, they turned the pipe into 1-1/2" diameter, and (ii) a 200mm x 200mm x 5mm thick steel plate for crane's footing they random minimized the size to be 150mm x 200mm (see picture). What a have!
-
Sometimes, not only to me, all of yours living in the world have need to accept and understand to other parties, you must plunge your heart into their hearts, adjust or amend the standard a little bit in order to create a harmonic space. As a matter of fact, I could not address any unsatisfaction or objection to the manufacturer as the price they quoted before was very cheap.
-
(4) Calculations and Decision Making
Free Body Diagram of the Lifting Crane:
Free Body Diagram of the Lifting Crane:
-
Weights:
Wt (Weight of the trolley)= 12Kg (Given by manufacturer)
Wb (Weight of the boom –1-1/2” pipe) = (4Kg/m x 0.275m) = 1.1Kg
We (Weight of the boom extension – 1-1/4” pipe) = (3.4Kg/m x 0.425m)= 1.445Kg
Wc (Weight of the Crane)= 20.162Kg
1. For 1-1/2” Main Boom (0.375m x 4kg/m)= 1.5Kg
2. For Winch System (6.5Kg)
3. For 2” Main Mast (0.865m x 5.41kg/m)= 4.671Kg
4. For Base Plate = 0.2m x 0.2m x 0.005m x 7874kg/m3 = 3.15kg
5. For 0.3m long Hollow Shaft for Base Plate (0.3m x 5.4kg/m)= 1.62Kg
6. For Metal Gill Covers (0.13m x 0.13m x 0.005m x 7874kg/m3 (Density) x 2) = 1.33Kg
7. For U channel (0.088m x 0.098m x 0.005 x 7874kg/m3 x 2)+(0.066m x 0.098m x 0.005m x 7874kg/m3 = 0.895Kg
8. For Fixing Plate (0.14m x 0.09m x 0.005m x 7874kg/m3)= 0.496Kg
Total Weight for Wc = 20.162Kg
-
The weights of the load and pipes multiplied by their respective distances forward from the tipping point must be equalized by the weights of the counterweight and crane net capacity multiplied by their respective distances rearward from the tipping point (LHS = RHS, See Figure 1, 2 & 3). Any variation caused by changing the radius at which the load is lifted destroys this equilibrium.
Roughly speaking, a balanced condition of my lifting crane shall be achieved by equalizing forward and rearward moments, say LHS = RHS. Let’s see the conditions.
-
Wt (Weight of the trolley)= 12Kg (Given by manufacturer)
Wb (Weight of the boom –1-1/2” pipe) = (4Kg/m x 0.275m) = 1.1Kg
We (Weight of the boom extension – 1-1/4” pipe) = (3.4Kg/m x 0.425m)= 1.445Kg
Wc (Weight of the Crane)= 20.162Kg
1. For 1-1/2” Main Boom (0.375m x 4kg/m)= 1.5Kg
2. For Winch System (6.5Kg)
3. For 2” Main Mast (0.865m x 5.41kg/m)= 4.671Kg
4. For Base Plate = 0.2m x 0.2m x 0.005m x 7874kg/m3 = 3.15kg
5. For 0.3m long Hollow Shaft for Base Plate (0.3m x 5.4kg/m)= 1.62Kg
6. For Metal Gill Covers (0.13m x 0.13m x 0.005m x 7874kg/m3 (Density) x 2) = 1.33Kg
7. For U channel (0.088m x 0.098m x 0.005 x 7874kg/m3 x 2)+(0.066m x 0.098m x 0.005m x 7874kg/m3 = 0.895Kg
8. For Fixing Plate (0.14m x 0.09m x 0.005m x 7874kg/m3)= 0.496Kg
Total Weight for Wc = 20.162Kg
-
The weights of the load and pipes multiplied by their respective distances forward from the tipping point must be equalized by the weights of the counterweight and crane net capacity multiplied by their respective distances rearward from the tipping point (LHS = RHS, See Figure 1, 2 & 3). Any variation caused by changing the radius at which the load is lifted destroys this equilibrium.
Roughly speaking, a balanced condition of my lifting crane shall be achieved by equalizing forward and rearward moments, say LHS = RHS. Let’s see the conditions.
-
Condition 1:
Weight of the tortoise = 100Kg (Maximum Working Load)
Distance between the centerline of the filler and the line of tipping point =0.375m (225mm + 150mm)
(Filler x 0.375m)+(20.162Kg x 0.225m)+(12Kg x 0.25m)=(1.1Kg x 0.1375m)+(1.5Kg x 0.2125m)+(100Kg x 0.425m)
(Filler x 0.375m)+4.537kgm+3kgm = 0.151kgm+0.319kgm+42.5kgm
(Filler x 0.375m)+7.537kgm = 42.97kgm
Filler = 94.49kg (not recommended)
-
Condition 2:
Weight of the tortoise = 50Kg (Maximum Working Load)
Distance between the centerline of the filler and the line of tipping point =0.375m (225mm + 150mm)
(Filler x 0.375m)+(20.162Kg x 0.225m)+(12Kg x 0.25m)=(1.1Kg x 0.1375m)+(1.5Kg x 0.2125m)+(50Kg x 0.425m)
(Filler x 0.375m)+4.537kgm+3kgm = 0.151kgm+0.319kgm+21.25kgm
(Filler x 0.375m)+7.537kgm = 21.72kgm
Filler = 37.82kg
-
By calculation, a 50Kg (see condition 2) load at a 425mm radius gives a forward load moment of 21.72kgm. This load moment would then be equalized or counterbalanced by a 37.82kg counterweight at a distance of 375mm, having rearward load moment of 21.72kgm.
According to the condition 1, if the weight of the load were to be doubled (say 100kg), the weight of the counterweight must also be tripled to keep the crane in balance. By so doing, adding a considerable amount of filler to keep the crane in balance is neither practical nor economic to my budget. Not to say money, a bulky weight will certainly make the crane unlovely, and it will be less likely to be accepted by any and every designer or engineer. As such, the maximum working load of my crane, in my final decision despite of how much i am unwilling, will be downgraded and only operate for a rated load of 50kg.
-
Take Moment at Rf (Condition 2)
+ ↘(Σ M)Rf = 0:
(Wc x 0.225m)+(Wt x 0.25m)+(Filler x 0.375m)–(Rr x 0.45m)–(Wb x 0.1375m)–(We x 0.2125m)–(Weight of Tortoise x 0.425m)= 0
(20.162Kg x 0.225m)+(12Kg x 0.25m)+(Filler x 0.375m)–(Rr x 0.45m)–(1.1Kg x 0.1375m)–(1.5Kg x 0.2125m)–(50Kg x 0.425m) =0
4.536Kgm+3Kgm+(Filler x 0.375m)–(Rr x 0.45m)–(0.1513Kgm)–0.319Kgm–21.25kgm=0
-14.184kgm+(Filler x 0.375m)–(Rr x 0.45m)=0
Rr x 0.45m = (Filler x 0.375m) -14.184kgm
Rr = <(Filler x 0.375m) –14.184kgm> / 0.45m
Rr = 0.833Filler – 31.52kg
-
Take Moment at Rr (Condition 2)
+ ↘(Σ M)Rr = 0:
(Rf x 0.45m)-(50kg x 0.875m)-(1.5kg x 0.6625m)-(1.1Kg x 0.5875m)–(20.162Kg x 0.225m)–(12Kg x 0.2m)–(Filler x 0.075m) =0
(Rf x 0.45m)- (43.75kgm)–(0.994kgm)–(0.6463kgm)–(4.536kgm)–(2.4kgm)–(Filler x 0.075m) =0
(Rf x0.45m)–52.33kgm–(Filler x 0.075m)=0
Rf x 0.45m = 52.33kgm + (Filler x 0.075m)
-
As can be seen the calculation previously, a 50Kg load at a 425mm radius gives a forward load moment of 21.72kgm, this would then be equalized by a 37.82kg weight, (Filler = 37.82kg)
-
When the weight at the filler's side is 37.82kg (Condition 2), Rf & Rr would be obtained:
Rr = 0.833Filler – 31.52kg
Rr = 0.833 (37.82kg) – 31.52kg
Rr = -0.016kg
Rf x 0.45m = 52.33kgm + (Filler x 0.075m)
Rf x 0.45m = 52.33kgm + (37.82kg x 0.075m)
Rf = 122.59kg
-
In the case of Condition 2, fillers weighting 37.82kg require being loaded on the counterweight frame; two front wheels Rf need to withstand a downward force 122.59kg. As per the calculation, each front wheel requires to saddle with the related downward force 61.3kg (122.59kg/2).
In terms of the value for Rr, it is a negative value and means that the rear side of the trolley may be easily raised because the entire loads are concentrated on the front wheels when the crane is operated. To make it steady, I will round off the filler to be 40Kg, then the values of Rr and Rf will be changed slightly to 1.8Kg and 120.77kg respectively.
Weight of the tortoise = 100Kg (Maximum Working Load)
Distance between the centerline of the filler and the line of tipping point =0.375m (225mm + 150mm)
(Filler x 0.375m)+(20.162Kg x 0.225m)+(12Kg x 0.25m)=(1.1Kg x 0.1375m)+(1.5Kg x 0.2125m)+(100Kg x 0.425m)
(Filler x 0.375m)+4.537kgm+3kgm = 0.151kgm+0.319kgm+42.5kgm
(Filler x 0.375m)+7.537kgm = 42.97kgm
Filler = 94.49kg (not recommended)
-
Condition 2:
Weight of the tortoise = 50Kg (Maximum Working Load)
Distance between the centerline of the filler and the line of tipping point =0.375m (225mm + 150mm)
(Filler x 0.375m)+(20.162Kg x 0.225m)+(12Kg x 0.25m)=(1.1Kg x 0.1375m)+(1.5Kg x 0.2125m)+(50Kg x 0.425m)
(Filler x 0.375m)+4.537kgm+3kgm = 0.151kgm+0.319kgm+21.25kgm
(Filler x 0.375m)+7.537kgm = 21.72kgm
Filler = 37.82kg
-
By calculation, a 50Kg (see condition 2) load at a 425mm radius gives a forward load moment of 21.72kgm. This load moment would then be equalized or counterbalanced by a 37.82kg counterweight at a distance of 375mm, having rearward load moment of 21.72kgm.
According to the condition 1, if the weight of the load were to be doubled (say 100kg), the weight of the counterweight must also be tripled to keep the crane in balance. By so doing, adding a considerable amount of filler to keep the crane in balance is neither practical nor economic to my budget. Not to say money, a bulky weight will certainly make the crane unlovely, and it will be less likely to be accepted by any and every designer or engineer. As such, the maximum working load of my crane, in my final decision despite of how much i am unwilling, will be downgraded and only operate for a rated load of 50kg.
-
Take Moment at Rf (Condition 2)
+ ↘(Σ M)Rf = 0:
(Wc x 0.225m)+(Wt x 0.25m)+(Filler x 0.375m)–(Rr x 0.45m)–(Wb x 0.1375m)–(We x 0.2125m)–(Weight of Tortoise x 0.425m)= 0
(20.162Kg x 0.225m)+(12Kg x 0.25m)+(Filler x 0.375m)–(Rr x 0.45m)–(1.1Kg x 0.1375m)–(1.5Kg x 0.2125m)–(50Kg x 0.425m) =0
4.536Kgm+3Kgm+(Filler x 0.375m)–(Rr x 0.45m)–(0.1513Kgm)–0.319Kgm–21.25kgm=0
-14.184kgm+(Filler x 0.375m)–(Rr x 0.45m)=0
Rr x 0.45m = (Filler x 0.375m) -14.184kgm
Rr = <(Filler x 0.375m) –14.184kgm> / 0.45m
Rr = 0.833Filler – 31.52kg
-
Take Moment at Rr (Condition 2)
+ ↘(Σ M)Rr = 0:
(Rf x 0.45m)-(50kg x 0.875m)-(1.5kg x 0.6625m)-(1.1Kg x 0.5875m)–(20.162Kg x 0.225m)–(12Kg x 0.2m)–(Filler x 0.075m) =0
(Rf x 0.45m)- (43.75kgm)–(0.994kgm)–(0.6463kgm)–(4.536kgm)–(2.4kgm)–(Filler x 0.075m) =0
(Rf x0.45m)–52.33kgm–(Filler x 0.075m)=0
Rf x 0.45m = 52.33kgm + (Filler x 0.075m)
-
As can be seen the calculation previously, a 50Kg load at a 425mm radius gives a forward load moment of 21.72kgm, this would then be equalized by a 37.82kg weight, (Filler = 37.82kg)
-
When the weight at the filler's side is 37.82kg (Condition 2), Rf & Rr would be obtained:
Rr = 0.833Filler – 31.52kg
Rr = 0.833 (37.82kg) – 31.52kg
Rr = -0.016kg
Rf x 0.45m = 52.33kgm + (Filler x 0.075m)
Rf x 0.45m = 52.33kgm + (37.82kg x 0.075m)
Rf = 122.59kg
-
In the case of Condition 2, fillers weighting 37.82kg require being loaded on the counterweight frame; two front wheels Rf need to withstand a downward force 122.59kg. As per the calculation, each front wheel requires to saddle with the related downward force 61.3kg (122.59kg/2).
In terms of the value for Rr, it is a negative value and means that the rear side of the trolley may be easily raised because the entire loads are concentrated on the front wheels when the crane is operated. To make it steady, I will round off the filler to be 40Kg, then the values of Rr and Rf will be changed slightly to 1.8Kg and 120.77kg respectively.
------------------------------------------------------------------------------------------------
Alternatively, the counterweight can be moved further rearward from the centerline of tipping to compensate for the load, it can minimize the amount of the filler. Let's see the change.
(1st Trial) Moving back the whole crane about 50mm:
If one small adjustment is made in the design, the crane is shifted slightly back from the line of tipping point; a gain will be obtained at the rearward moment. Let’s see the condition 3 and 4.
-
-
Condition 3:
Weight of the tortoise = 50Kg,
Distance between the centerline of the filler and the line of tipping point =0.425m (275mm + 150mm)
(Filler x 0.425m)+(20.162Kg x 0.275m)+(12Kg x 0.3m) = (1.1Kg x 0.0875m)+(1.5Kg x 0.1625m)+(50Kg x 0.375m)
(Filler x 0.425m)+5.54455kgm+3.6kgm = 0.09625kgm+0.24375kgm+18.75kgm
(Filler x 0.425m) = 9.94545kgm
Filler = 23.4kg
-
Obviously, the gain at the rear moment has been obtained, moving the crane about 50mm rearward from the line of tipping point can free from 14.42kg for the filler (37.82Kg – 23.4Kg).
-
Take Moment at Rf (Condition 3)
If the weight of the filler is 23.4kg (Condition 3), then Rf & Rr would be obtained:
(20.162Kg x 0.275m)+(12Kg x 0.3m)+(Filler x 0.425m)–(Rr x 0.45m)–(1.1Kg x 0.875m)–(1.5Kg x 0.1625m)–(50Kg x 0.375m) =0
Rr x 0.45m = (Filler x 0.425m) -10.812kgm
Rr = <(Filler x 0.425m)-10.812kgm> / 0.45m
Rr = <(23.4kg x 0.425m)-10.812kg> / 0.45m
Rr = -1.93kg
-
Take Moment at Rr (Condition 3)
+ ↘(Σ M)Rr = 0:
(Rf x 0.45m)–(50kg x 0.825m)–(1.5kg x 0.6125m)–(1.1Kg x 0.5375m)–(20.162Kg x 0.175m)–(12Kg x 0.15m)–(Filler x 0.05m) =0
(Rf x 0.45m)–(41.25kgm)–(0.92kgm)–(0.59kgm)–(3.53kgm)–(1.8kgm)-(Filler x 0.05m) =0
(Rf x0.45m)–48.09kgm–(Filler x 0.05m)=0
Rf x 0.45m = 48.09kgm+(Filler x 0.05m)
Rf = <48.09> / 0.45m
Rf = 109.47kg
-
Condition 4:
Weight of the tortoise = 15Kg
Distance between the centerline of the filler and the line of tipping point =0.425m (275mm + 150mm)
(Filler x 0.425m)+(20.162Kg x 0.275m)+(12Kg x 0.3m) = (1.1Kg x 0.0875m)+(1.5Kg x 0.1625m)+(15Kg x 0.375m)
(Filler x 0.425m)+5.54455kgm+3.6kgm = 0.09625kgm+0.24375kgm+5.625kgm
(Filler x 0.425m) = 9.94545kgm
Filler = -0.134kg
-
Take Moment at Rf (Condition 4)
If the weight of the filler is –0.134kg (Condition 3), then Rf & Rr would be obtained:
(20.162Kg x 0.275m)+(12Kg x 0.3m)+(Filler x 0.425m)-(Rr x 0.45m)–(1.1Kg x 0.875m)–(1.5Kg x 0.1625m)–(15Kg x 0.375m) =0
5.545Kgm+3.6Kgm+(Filler x 0.425m)–(Rr x 0.45m)–(0.963Kgm)–0.244Kgm–5.625kgm=0
2.313kgm+(Filler x 0.425m)-(Rr x 0.45m)=0
Rr x 0.45m = (Filler x 0.425m)+2.313kgm
Rr = <(Filler x 0.425m)+2.313kgm> / 0.45m
Rr = <(-0.134kg x 0.425)+2.313kg> / 0.45m
Rr = 5.0134kg
-Take Moment at Rr (Condition 3)
+ ↘(Σ M)Rr = 0:
(Rf x 0.45m)–(50kg x 0.825m)–(1.5kg x 0.6125m)–(1.1Kg x 0.5375m)–(20.162Kg x 0.175m)–(12Kg x 0.15m)–(Filler x 0.05m) =0
(Rf x 0.45m)–(41.25kgm)–(0.92kgm)–(0.59kgm)–(3.53kgm)–(1.8kgm)-(Filler x 0.05m) =0
(Rf x0.45m)–48.09kgm–(Filler x 0.05m)=0
Rf x 0.45m = 48.09kgm+(Filler x 0.05m)
Rf = <48.09> / 0.45m
Rf = 109.47kg
-
Condition 4:
Weight of the tortoise = 15Kg
Distance between the centerline of the filler and the line of tipping point =0.425m (275mm + 150mm)
(Filler x 0.425m)+(20.162Kg x 0.275m)+(12Kg x 0.3m) = (1.1Kg x 0.0875m)+(1.5Kg x 0.1625m)+(15Kg x 0.375m)
(Filler x 0.425m)+5.54455kgm+3.6kgm = 0.09625kgm+0.24375kgm+5.625kgm
(Filler x 0.425m) = 9.94545kgm
Filler = -0.134kg
-
Take Moment at Rf (Condition 4)
If the weight of the filler is –0.134kg (Condition 3), then Rf & Rr would be obtained:
(20.162Kg x 0.275m)+(12Kg x 0.3m)+(Filler x 0.425m)-(Rr x 0.45m)–(1.1Kg x 0.875m)–(1.5Kg x 0.1625m)–(15Kg x 0.375m) =0
5.545Kgm+3.6Kgm+(Filler x 0.425m)–(Rr x 0.45m)–(0.963Kgm)–0.244Kgm–5.625kgm=0
2.313kgm+(Filler x 0.425m)-(Rr x 0.45m)=0
Rr x 0.45m = (Filler x 0.425m)+2.313kgm
Rr = <(Filler x 0.425m)+2.313kgm> / 0.45m
Rr = <(-0.134kg x 0.425)+2.313kg> / 0.45m
Rr = 5.0134kg
Calculate the value of Rf (Condition 4)
Rf + Rr = 15kg + 1.1kg + 1.5kg + 20.162kg + 12kg + (-0.134kg)
Rf = -Rr + 49.628
Rf = -5.0134 + 49.628
Rf = 44.615kg
Rf + Rr = 15kg + 1.1kg + 1.5kg + 20.162kg + 12kg + (-0.134kg)
Rf = -Rr + 49.628
Rf = -5.0134 + 49.628
Rf = 44.615kg
------------------------------------------------------------------------------------------------
(2nd Trial) Turning the lifting crane at different degrees
(2nd Trial) Turning the lifting crane at different degrees
-
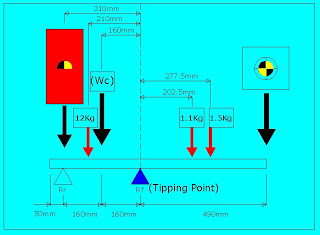
Condition 3a:
Weight of the tortoise = 15Kg
Distance between the centerline of the filler and the line of tipping point=0.31m.
(Filler x 0.31m)+(20.162Kg x 0.16m)+(12Kg x 0.21m) = (1.1Kg x 0.2025m)+(1.5Kg x 0.2775m)+(15Kg x 0.49m)
(Filler x 0.375m)+3.226kgm+2.52kgm = 0.223kgm+0.416kgm+7.35kgm
(Filler x 0.375m)+5.746kgm = 7.989kgm
Filler = 5.98kg
-
Take Moment at Rf
+ ↘(Σ M)Rf = 0:
(Wc x 0.16m)+(Wt x 0.21m)+(Filler x 0.31m)-(Rr x 0.32m)–(Wb x 0.202m)-(We x 0.2775m)–(Weight of Tortoise x 0.49m)= 0
3.23Kgm+2.52kgm+1.854kgm–(Rr x 0.32m)-0.222kgm–0.4163kgm–7.35kgm =0
Rr x 0.32m = -0.384kgm
Rr = -0.384kgm> / 0.32m
Rr = -1.2kg
-
Total upward forces = Total downward forces
20.162kg + 12Kg + 5.98kg + 1.1kg +1.5kg + 15Kg = -1.2kg + Rf
Rf = 56.942Kg
-
In the case of Condition 3a, fillers weighting 5.98kg are needed to load on the counterweight frame; the front wheels Rf need to withstand a downward force 56.942kg. As per the calculation, each front wheel requires to saddle with the related downward force 56.942kg/2.
To get rid of the problem on counterbalance, the makeshift to make the crane steady was that I put a chain weighting 8Kg into the metal case (Counterweight), the values of Rr and Rf will be changed slightly to 0.76kg and 57Kg respectively. As it has been mentioned early, the negative in the value of Rr represents a little force that can easily overturn the crane.
-
-
-
All in all, I must give tribute to all those who helped me to make my crane work, to make my dream coming true, as well to understand more on the principle of Mechanical Engineering Design.
-
Best Regards
Ken Ngan
P.S.: Super-Ken 2000 is a humanoid crane, I can feel its heart beating!
No comments:
Post a Comment